Transformer之位置编码

为什么需要位置编码

注意力计算公式如下图所示：

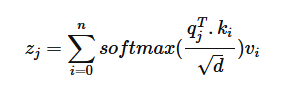
其中q和k分别为query和key，代表token的语义信息。如果没有位置编码，那么q和k的计算结果是不受二者之间相对距离大小的影响的。也就是说，如果没有位置编码，那么transformer就是一个类词袋模型。

词袋模型

词袋模型：BOW，是一种对文本进行向量化的模型
词袋模型首先会对文本进行分词，为所有出现过的词给定一个序号，进而得到一个语料库，比如语料库大小为1000。则对于一个句子比如“我爱你”进行语义建模，由于这三个字在语料库中的序号为333，335，874.则这句话的语义向量为：[0,0,0,0,0,...1,0,0,1,0,...,1,0,0,0,0]即在对应索引处置1即可。这样带来一个问题即’你爱我’和’我爱你’这两句意思不同的话的语义向量是相同的。所以，词袋模型不考虑词语顺序，只是将词一股脑儿的放进袋子里，根据句子内词语出现的次数来进行语义建模。

Attention机制的缺陷

attention机制是transformer的核心，其思想是计算每个token与其余token的相似度，利用这个相似度去更新token的语义。从上面的计算公式可以看出，这种相似度计算是全局的，是位置无关的，无论两个token是相近还是相远，注意力分数都是一样的。下面这个代码将这个特性展现了出来：

import torch
import torch.nn.functional as F
d = 8 # 词嵌入维度
t = 3 # 句子长度
q = torch.randn(1,d) # 我
k = torch.randn(t,d) # 我爱你
v = torch.randn(t,d) # 我爱你

w = q@k.transpose(1,0)
w1 = F.softmax(w,dim=1)
result = w1 @ v

k_shift = k[[2,1,0],:] # 你爱我
v_shift = v[[2,1,0],:] # 你爱我
shift_w = q@k_shift.transpose(1, 0)
shift_w1 = F.softmax(shift_w, dim=1)
shift_result = shift_w1 @ v_shift

print(torch.allclose(result, shift_result))
True

即’我’在我爱你和你爱我中的语义是一样的，这是肯定不对的。所以，就需要我们在transformer中添加位置编码，让模型在计算token之间的相似度时，能知晓两个token之间的相对距离

有几种位置编码

位置编码主要分为两种，第一种是想办法将位置信息融入到输入中，这是绝对位置编码的一般做法。另一种是修改一下Attention机制的结构，使其能够在计算注意力分数时，考虑到位置信息，这构成了相对位置编码的一般做法。我们首先介绍一下绝对位置编码。

绝对位置编码

其公式如下：

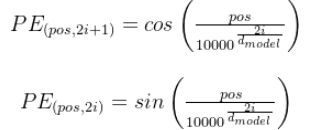
其中pos代表单个token的位置索引，比如1000个token，这个pos的取值则为0-999。i表示同一个token的向量的某一个维度索引，其中偶数维都有sin函数计算，奇数维都由cos函数计算。其代码如下所示：

class PositionEncoding(nn.Module):
    def __init__(self, d_model, dropout, max_len=5000):
        super().__init__()
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)  ## (max_len, 1)
        div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))  ## d_model/2 中结果

        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)  ## 在第一个维度添加一个维度，便于批处理  (1, max_len, d_model)
        self.register_buffer('pe', pe)
    
    def forward(self, x):
        x = x + torch.tensor(self.pe[:, :x.size(1)], requires_grad=False)  ## max_len是模型能接受的最大长度token输入，推理时token长度是不定的，x.size()是B,T,C
        ## x.size(1)是输入的token长度，则将输入token长度对应的位置编码加入到计算中
        return self.dropout(x)

为什么要使用这种sin和cos交替的形式来表示一个token的位置信息呢？transformer作者在论文中并没有明说。但是根据公式的形式，我们可以发现这个位置编码的几个性质：

有界性：sin函数和cos函数都是有界的，所以位置编码的值不会太大也不会太小，在-1到1的范围之内
周期性：不同token的同一个维度的位置编码值可以看作是同一个频率的正余弦向量，因为分母是一样大的，只是分子不同。即一个1000维的位置向量，其低维处的变量是高频频变化的，高维处的变量是低频变化的。周期性可以使得位置编码在处理较长的序列时，仍然能生成合理的值。
叠加性：对于同一个token而言，每两个不同的维度对，比如0-1和2-3，都是不同频率的正余弦向量在同一个点处的值。任意周期函数都可以用傅里叶展开公式变为三角函数的无穷级数。这里可以用这种方式理解，即叠加不同频率的正余弦函数，试图表示token的位置信息
能够反映一定的相对位置：PE(x+k)可以用PE(x)来线性表示。因为sin(x+k)=sin(x)cosk + cos(x)sink，其中sink和cosk看作常数。即给定距离k和当前位置，k距离处的位置编码是当前位置关于距离k的线性组合
远程衰减：两个位置编码的点积取决于二者之间的相对位置，即两个位置编码的点积值可以反映其相对位置的大小。由下图可知，当相对位置增大时，点积的值是在减小的。而且这种点积具有对称性。
综上所述，绝对位置编码能够反映token之间的绝对位置信息，同时也能够一定程度上反映token之间的相对位置。

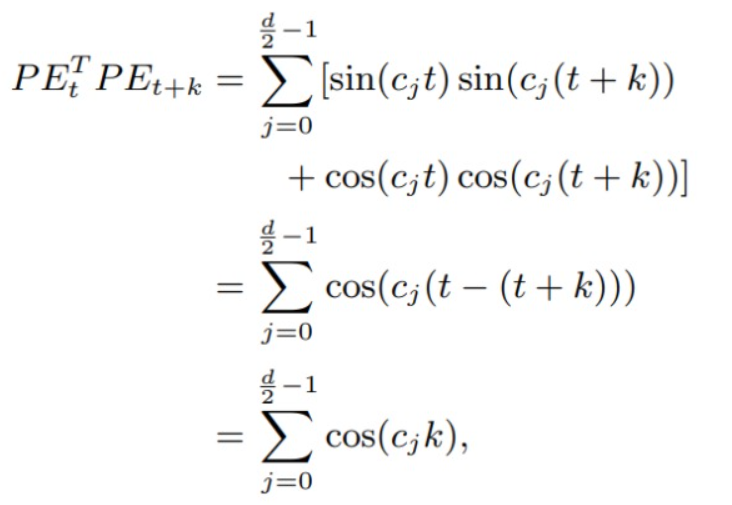
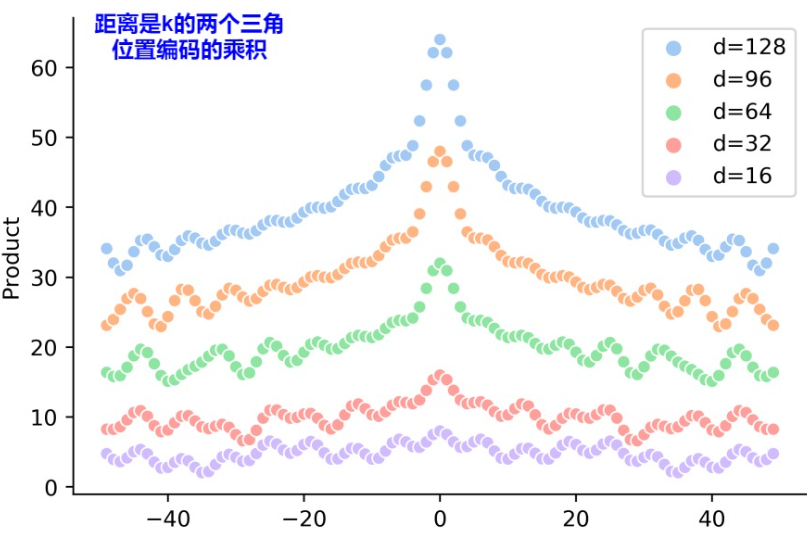
所以，综上所述，绝对位置编码能够较好的表示token的位置信息，同时，也能够表示一定的相对位置信息。但是在实际使用中，绝对位置编码的外推性和远程衰减的特性都不能很好的展现。原因如下：

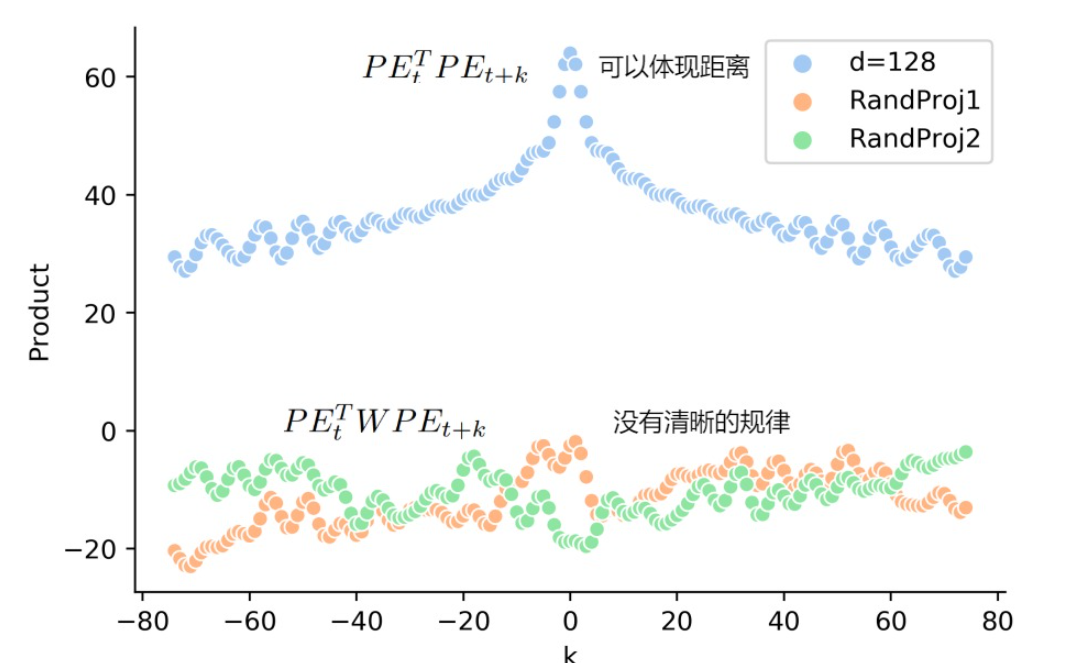
由上图可知，位置编码是和word_embedding加和在一起的，经过注意力层的Q和K点积之后，其远程衰减的特性消失了，那么其表达相对位置的能力就不存在了。Q和K点积的公式如下：

$$
\begin{align*}
q_{t}^{T} * k_{t+\Delta t} = \left[W_{Q} * (x_{t} + PE_{t})\right]^{T} \left[W_{K} * (x_{t+\Delta t} + PE_{t+\Delta t})\right] = \left[x_{t}^{T} W_{Q}^{T} + PE_{t}^{T} W_{Q}^{T}\right] \left[W_{K} x_{t+\Delta t} + W_{K} PE_{t+\Delta t}\right]
\end{align*} \tag{1.1}
$$

由公式可知，q与一个相距为$\Delta t$的k相乘的结果是$x_{t}^TW_{Q}^TW_{K}x_{t + \Delta t}$，这一部分是注意力分数，后面的部分都是加性的绝对位置编码的带来的部分，由图4可知，这种冗余部分破坏了位置编码的相对位置属性，所以这就是绝对位置编码在注意力计算中无法表达相对位置信息的原因，也是加性的位置编码的弊端。

旋转位置编码

为了解决加性位置编码的弊端，之后便出现了乘性的位置编码。旋转位置编码的思想是使用相乘的方法令每一个token都含有自己的绝对位置信息，那么在两个token相乘的时候，结果中自动的就会包含了相对位置信息。

首先我们需要回顾一下线性代数中旋转矩阵的知识。维基百科定义为：旋转矩阵是在乘以一个向量的时候，改变了向量的方向但不改变向量大小的矩阵。在二维空间中，旋转矩阵表示如下：

$$
M(\theta) = \begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix} \tag{1.2}
$$

$M(\theta)$就是一个旋转矩阵，由三角函数的和角公式，我们可以得到两个旋转矩阵相乘的结果为：

$$
M(\theta)^T \cdot M(\alpha) = \begin{bmatrix}
\cos\theta & \sin\theta \\
-\sin\theta & \cos\theta
\end{bmatrix} \cdot \begin{bmatrix}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{bmatrix} = \begin{bmatrix}
\cos(\alpha - \theta) & -\sin(\alpha - \theta) \\
\sin(\alpha - \theta) & \cos(\alpha - \theta)
\end{bmatrix} = M(\alpha - \theta) \tag{1.3}
$$

由上式可知，两个带有旋转角度信息的旋转矩阵进行向量乘法，其结果就带有了相对信息。那么如果我们对每一个token都旋转一个角度，这个角度与其绝对位置有关，之后进行qk相乘的时候，注意力分数中就会带有相对位置信息。公式如下：
$$
(R_m \cdot x)^T * (R_n \cdot y) = x^T \cdot R_m^T \cdot R_n \cdot y = x^T \cdot R_{n-m} \cdot y \tag{1.4}
$$

那么既然相对位置信息是在query和key相乘的时候自动添加的，那么关键就在于如何为每个token的query和key向量添加绝对位置信息。其实很简单，将每个query和key向量，旋转位置索引个单位角度$\theta$即可。则注意力公式变为：
$$
Attention(q_m, k_n) = (R_m \cdot q_m)^T \cdot (R_n \cdot k_n) \tag{1.5}
$$
其中$R_m$等于如下：
$$
R_m = \begin{bmatrix}
\cos m\theta & -\sin m\theta \\
\sin m\theta & \cos m\theta
\end{bmatrix} \tag{1.6}
$$
m为qk的位置索引，即pos，$\theta$仍然沿用正余弦绝对位置编码的设置即：
$$
\theta_i = 10000^{-2i/d} \tag{1.7}
$$
如果query和key不是二维呢？在实际的transformer中，q和k都是高维向量，那么对于高维的向量，我们将其维度两两分为一组，比如1000维的query向量，$q_0$和$q_1$可以看作一组，令其与式(1.6)相乘，则将这一组向量赋予了绝对位置信息。公式如下：
$$
\mathbf{R_m \cdot q_m} = \begin{bmatrix}
\cos m\theta_0 & -\sin m\theta_0 \\
\sin m\theta_0 & \cos m\theta_0
\end{bmatrix} \cdot \begin{bmatrix}
\ q_0 \\
\ q_1
\end{bmatrix} \tag{1.8}
$$
所以，对于一整个高维的query向量来说，都两两乘以一个旋转矩阵，如图下：

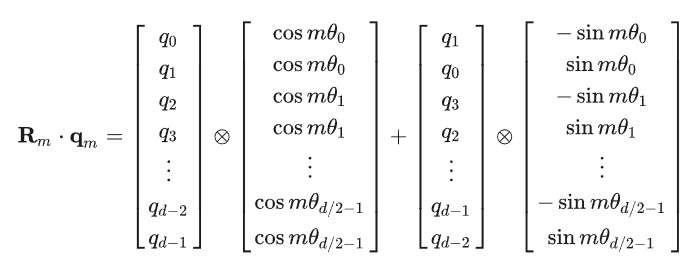
上式相当于使用一个高维的，稀疏的，对角矩阵乘以query向量，当然我们不会创建整个稀疏矩阵，太大太占用内存了。所以对于一个1000维的query而言，我们可以首先计算上图中的cos和sin的部分，假如整个token序列的最大长度为500，m取值为0-499，$\theta$的指数部分取值为：(0, 2, 4, .....,994, 996, 998) / 1000，得到上图中的cos_table和sin_table, 都为一个$500 \cdot 1000$的矩阵。对于每一个$q_m$,乘以cos_table和sin_table中对应位置的$1 \cdot 1000$的向量即可。代码如下：

def create_sin_cos_cache(max_num_tokens, head_size):
    theta = 10000 ** (-np.arange(0, head_size, 2) / head_size)
    theta = theta.reshape(-1, 1).repeat(2, axis=1).flatten()

    pos = np.arange(0, max_num_tokens)
    table = pos.reshape(-1, 1) @ theta.reshape(1, -1)  # [max_num_tokens, head_size]

    sin_cache = np.sin(table)
    sin_cache[:, ::2] = -sin_cache[:, ::2]

    cos_cache = np.cos(table)
    return sin_cache, cos_cache

def rotate_half(vec):
    return vec.reshape(-1, 2)[:, ::-1].flatten()

def rotary(vec, pos, sin_table, cos_table):
    return vec * cos_table[pos] + rotate_half(vec) * sin_table[pos]

其实，通过旋转的方式注入绝对位置信息这种办法，在正余弦位置编码中也可以体现。假设$c_i = 1 / 10000^{-2i/d}$,那么第t个位置的绝对位置编码可以表示为：
$$
PE_t = \begin{bmatrix}
\sin t \cdot c_i \\
\cos t\cdot c_i
\end{bmatrix} \tag{1.9}
$$

第$t + k$位置的绝对位置编码$PE_{t+k}$可以表示为：
$$
\begin{aligned}
PE_{t+k} &=
\begin{bmatrix}
\sin (t + k) \cdot c_i \\
\cos (t + k) \cdot c_i
\end{bmatrix}
\\
&=
\begin{bmatrix}
\sin (t \cdot c_i) \cdot \cos (k \cdot c_i) + \cos (t \cdot c_i) \cdot \sin (k \cdot c_i) \\
\cos (t \cdot c_i) \cdot \cos (k \cdot c_i) - \sin (t \cdot c_i) \cdot \sin (k \cdot c_i)
\end{bmatrix}
\\
&=
\begin{bmatrix}
\cos (k \cdot c_i) & \sin (k \cdot c_i) \\
-\sin (k \cdot c_i) & \cos (k \cdot c_i)
\end{bmatrix} \cdot \begin{bmatrix}
\sin (t \cdot c_i) \\
\cos (t\cdot c_i)
\end{bmatrix}
\\
&=
\begin{bmatrix}
\cos (k \cdot c_i) & \sin (k \cdot c_i) \\
-\sin (k \cdot c_i) & \cos (k \cdot c_i)
\end{bmatrix} \cdot PE_t
\end{aligned}
$$

将$c_i = 1 / 10000^{-2i/d}$视作一个常量，则$PE_t$和$PE_{t+k}$的关系为$PE_{t+k} = R_k^T \cdot PE_t$其中:
$$
R_k^T = \begin{bmatrix}
\cos (k \cdot c_i) & -\sin (k \cdot c_i) \\
\sin (k \cdot c_i) & \cos (k \cdot c_i)
\end{bmatrix}
$$

将上述公式展开如图下：

是不是和旋转位置编码很像？没错，绝对位置编码可以看作是使用旋转的方式将绝对位置信息注入位置编码中，但是，使用加和的方式破坏了位置信息的远程衰减特性，从而使得模型不能很好的识别相对位置信息。而旋转位置编码使用也是用旋转的方式将绝对位置信息注入到位置编码中，但其是在得到query和key之后注入的，这样后续的注意力计算可以直接利用旋转矩阵的性质而得到相对位置信息。

综上所述，旋转位置编码延续了绝对位置编码的一些特性，比如cos和sin的形式，只不过正余弦位置编码的三角函数中是$pos / (10000^{-2i/d})$而旋转位置编码中是$pos \cdot 10000^{-2i/d}$。正是因为如此，所以旋转位置编码也继承了远程衰减的特性。

二维旋转位置编码

对于一个句子里的token来说，一个数就可以表示其位置。那对于图片呢？图片中某个像素点的位置至少需要两个数才可确定，这是一维和二维的区别。其实和一维是一样的，其旋转矩阵公式如下：

$$
R_{x,y} =
\begin{bmatrix}
\cos x\theta & -\sin x\theta & 0 & 0 \\
\sin x\theta & \cos x\theta & 0 & 0 \\
0 & 0 & \cos y\theta & -\sin y\theta \\
0 & 0 & \sin y\theta & \cos y\theta
\end{bmatrix} \tag{1.10}
$$

可见，二维RoPE旋转矩阵是一维RoPE的分块矩阵。其和query向量的相乘方法和图7是一样的，所以实际上它相当于将输入向量分成了两半，一半施加x的一维RoPE，一般施加y的RoPE。由此我们不难推出三维和四维的做法。

源码中的RoPE

这里以chatglm的模型为例，模型设置如下：

config = GlmConfig(
    hidden_size=4096//2, 
    intermediate_size=13696, 
    num_hidden_layers=40//2, 
    num_attention_heads=32//2, 
    max_position_embeddings=131072)

将batch设置为1，token数设置为14，则hidden_states会输入到rotary_emb函数，如下：

1 2	## hidden_states : (1,14,2048) position_ids为一维数组，从0-13 position_embeddings = self.rotary_emb(hidden_states, position_ids)

这行代码会计算出图6中的cos和sin向量，根据绝对位置索引。其中position_embeddings是一个元组，包含了cos和sin，二者的大小都为(1,14,64)为什么是64呢，由上面的模型配置可知，注意力头数是16，隐藏层维度是2048，则每个头的维度为2048/16=128。即query向量的shape是(1,16,14,128)。但这也对不上啊，按照图6，cos和query向量的维度应该是一样的。别急，看下面的代码就知道了。

def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., 0::2]  ## 取出向量中的偶数索引
    x2 = x[..., 1::2]  ## 取出向量中的奇数索引 
    ## 将奇数索引加一个负号和偶数索引竖着堆好再展平，其实就是将图6第二部分sin的符号转移到query上面。
    return torch.stack((-x2, x1), dim=-1).flatten(-2)

def apply_rotary_pos_emb(q, k, cos, sin, position_ids=None, unsqueeze_dim=1):
    ## Applies Rotary Position Embedding to the query and key tensors.

    cos = cos.unsqueeze(unsqueeze_dim)  ## (1,14,64) -> (1,1,14,64)
    sin = sin.unsqueeze(unsqueeze_dim)

    # Interleave them instead of usual shape
    ## 操作cos和sin的最后一维，将最后一维截取一半并重复两次，
    ## 如果原始 cos 的最后一维是 [a, b, c, d]，经过上述操作后会变成 [a, a, b, b, c, c, d, d]。
    ## 大小仍为： (1,1,14,64)
    cos = cos[..., : cos.shape[-1] // 2].repeat_interleave(2, dim=-1)
    sin = sin[..., : sin.shape[-1] // 2].repeat_interleave(2, dim=-1)

    # Keep half or full tensor for later concatenation
    rotary_dim = cos.shape[-1]
    ## q_rot : (1,16,14,64) 即每个头只有一半的维度需要加入位置编码。
    q_rot, q_pass = q[..., :rotary_dim], q[..., rotary_dim:]
    k_rot, k_pass = k[..., :rotary_dim], k[..., rotary_dim:]

    # Apply rotary embeddings on the first half or full tensor
    ## 注入绝对位置信息
    q_embed = (q_rot * cos) + (rotate_half(q_rot) * sin)
    k_embed = (k_rot * cos) + (rotate_half(k_rot) * sin)

    # Concatenate back to full shape
    ## 将注入位置信息的部分和没有注入的部分合并
    q_embed = torch.cat([q_embed, q_pass], dim=-1)
    k_embed = torch.cat([k_embed, k_pass], dim=-1)
    return q_embed, k_embed

由代码q_rot和q_pass可知，和上面介绍的query的所有维度都做旋转变换不同，chatglm中只使用了前一半的维度来做旋转位置编码。为什么这么做呢？

旋转位置编码的核心思想是通过旋转操作嵌入位置信息，但并非所有维度都需要位置信息。
对于一些维度（如语义特征），位置信息可能无关紧要，因此可以直接跳过旋转操作。
这种分块处理方式既减少了计算开销，又保留了模型的灵活性。

这里值得注意的是key的shape:1,2,14,128，可见key向量只有2个头，而query有16个头。这和我们通常理解的MHA(Multi-head Attention)不同。是的，chatglm使用的是更流行的GQA：Group Query Attention，即多个query公用一个key，这里是8个query共用一个key。到时候key会通过复制操作变为1,16,14,128，但前八个是一样的，后八个也是一样的。后续会写一篇博客介绍注意力机制及其变体。

综上，我们总结了位置编码存在的意义以及几种常见的位置编码，目前旋转位置编码RoPE已经成为大模型的主流和标配，这也展现了其良好的性能。下次总结一下Normalization。我是punchy，下期再见。

参考连接

旋转式位置编码 (RoPE) 知识总结

探秘Transformer之（8）— 位置编码