为什么会有MLP？

transformer架构中，最主要的两个模块就是Attention-Layer和MLP-Layer。MLP全称为多层感知机，是神经网络的最主要的组成部分。其结构十分简单，主要由两层线性变换层和一个激活函数构成，其公式如下：

$$
MLP = \sigma(X \cdot W_1 + b_1) \cdot W_2 + b_2 \tag{1.1}
$$

在神经网络中，上述公式是构成整个模型基础，一个线性变换层则包括了上面的权重和偏置，通过引入激活函数来引入非线性，从而提高模型的非线性拟合能力。

既然MLP在神经网络中是通过引入非线性变换来提高模型的拟合高维空间的能力，那么在transformer中，MLP也是这样的作用，即：

通过线性变换层和激活函数，MLP能够将注意力机制的输出token进行非线性变换，从而捕捉token更复杂的语义，增强模型的表达能力。
token在经过attention层之后，其语义向量是涵盖了上下文信息的，MLP的作用就是进一步的去处理token的语义向量，帮助模型更好的理解向量中包含的上下文信息。这也是为什么transformer中Attention层之后就必须借一个MLP层，二者交替相接，重复多次，构成了模型的最重要的组成部分。

MLP的架构

而在transformer的MLP中，上不同的模型可能会在这个基础上添加一些dropout层来防止过拟合，或者添加gate层(门控投影)来进行一种门控操作。

下面以Llama的一个Base模型(0.8B)的MLP层为例，其内部结构如下图：

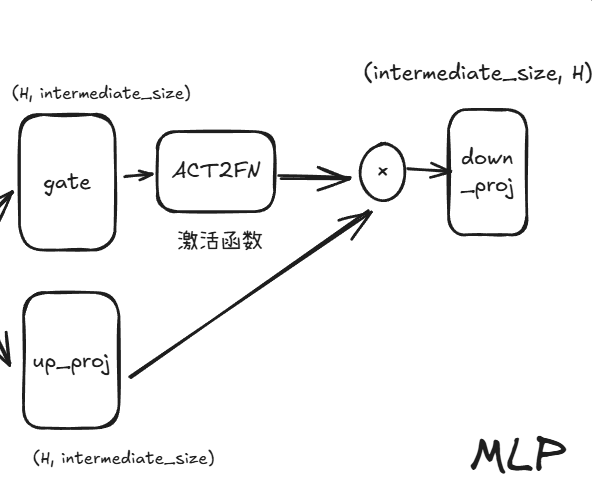
由上图可知，大小为H:4096的隐藏向量在进入MLP层时，会并行进入gate层和up_proj层，得到一个大小为intermediate_size:11008的中间向量，然后gate的输出经过ACT2FN，这是一个包含不同激活函数的字典，llama中使用的激活函数是silu，其函数图像如下：

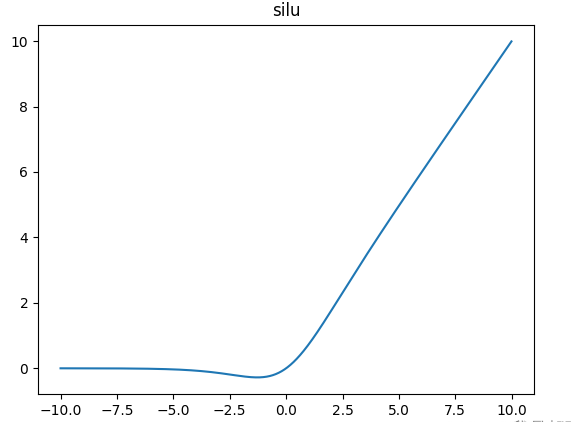
可以看到和relu函数很像，不同之处在于函数在过零点是更平滑一点，则零点附近的梯度不是像relu一样非零即1，则其同时具有relu的优点：避免梯度饱和区带来的可能的梯度消失。又避免了relu的缺点:零点梯度不存在且附近的梯度不够平滑。

经过激活函数后，gate层的输出和up_proj层的输出逐元素相乘，这样做的目的是可以通过gate层来控制up_proj层输出的高维向量的各个维度的值的大小，相当于乘以一个权重。这种操作可以让模型动态的调整MLP中高维向量的各个维度的权重，自主的选择哪些维度是重要的，哪些维度是不重要的。因为对于某些语义比较简单的token，使用一个11008维的向量来表达会过于冗余，过于复杂，这是如果模型能通过gate来抑制这个11008维向量的某些维度来表征这个简单语义的token，这样就可以降低模型的复杂度。

最后再经过一个down_proj将向量映射到低维。总的来说，MLP就是将token映射到高维，引入非线性，引入权重，在高维空间中捕捉token更复杂的语义信息后，再将token压缩至低维。

MoE

MoE的简史

MOE全称为：Mixture of Experts, 混合专家架构。随着LLM的发展，模型变得越来越大，参数变得越来越多，这对预训练带来了很多挑战，比如训练时间，比如显存占用。很多模型一张最好的GPU显卡都是放不下的，只能将模型切分，这同时会带来通信的问题。所以，MoE应运而生。

MoE的思想来源于集成学习，集成学习是通过训练多个模型即基学习器来解决同一个问题，将多个模型的预测结果简单的组合(投票或者平均)。集成学习的主要目标是通过减少过拟合，提高泛化能力，以提高预测性能。集成学习在训练过程中，利用训练数据集训练基学习器，基学习器的算法可以是决策树、SVM、线性回归、KNN等，在推理过程中对于输入的X，在每个基学习器得到相应的答案后将所有结果有机统一起来，例如通过求均值的方法解决数值类问题，通过投票方式解决分类问题。

MoE的的想法是，每个网络即专家，处理训练样本的不同子集，每个网络专注于输入空间的特定区域。那么如何选择哪个专家来处理哪个区域呢？这就是门控网络要决定的。

MoE的构成

MoE其实是对原本transformer中的MLP的替代，这里我们称原始的MLP为稠密的，因为MoE是稀疏的。为什么稀疏？看一下它的架构就知道了。如下图所示：

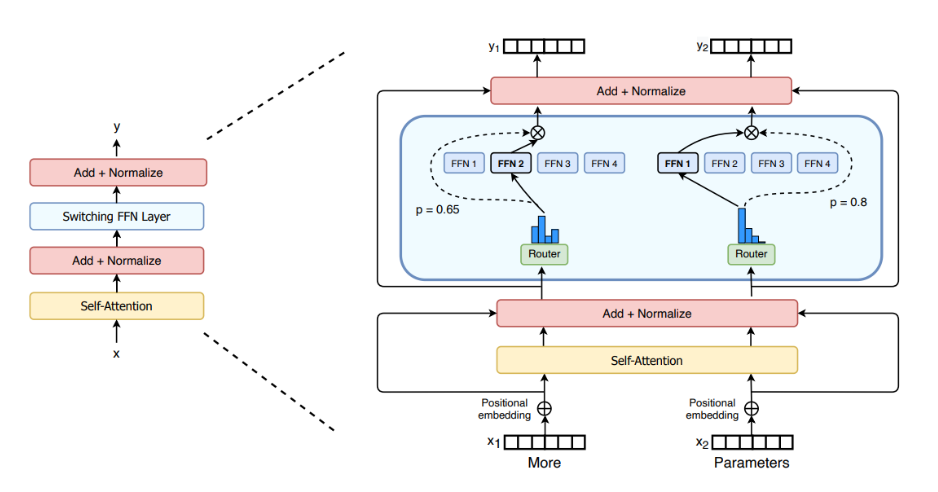
可以看到，一个门控网络Router的输入是token的语义向量，输出是一个概率。这个概率决定了这个token会被哪个FFN所处理。这就是MoE的实现办法。而FFN其实和MLP是一样的只是叫法不同，其代码如下：

class FeedForward(nn.Module):
    def __init__(self, dim_vector, dim_hidden, dropout=0.1):
        super().__init__()
        self.feedforward = nn.Sequential(
            nn.Linear(dim_vector, dim_hidden),
            nn.ReLU(),
            nn.Dropout(dropout),
            nn.Linear(dim_hidden, dim_vector)
        )
        
    def forward(self, x):
        out = self.feedforward(x)
        return out

门控网络是怎么实现的呢？其公式如下所示：

$$
G_{\sigma}(x) = Softmax(x \cdot W_g) \tag{1.2}
$$

就是输入经过一个线性变换后，再使用softmax将向量概率化。以TopK举例，假如有四个专家网络，我们取前2个概率最高的专家，那么门控网络会将一个4096维的向量变为一个4维的向量，softmax之后即是0-3这四个专家各自的概率，假如第0个和第3个专家的概率最大，分别为0.3和0.4，则该token会被送到第0个和第3个专家进行处理，二者的输出再加权求和，权重是被选中的专家的概率的分布，比如专家0的权重为：0.3/0.7 = 0.43。代码如下：

# 这里我们假设定义n_embed为32， num_experts=4, top_k=2

class TopkRouter(nn.Module):
    def __init__(self, n_embed, num_experts, top_k):
        super(TopkRouter, self).__init__()
        self.top_k = top_k
        self.linear =nn.Linear(n_embed, num_experts)
    
    def forward(self, mh_output):
        logits = self.linear(mh_output)    # (2,4,32) ---> (2,4,4)

        # #Noise logits
        # noise_logits = self.noise_linear(mh_output)

        # #Adding scaled unit gaussian noise to the logits
        # noise = torch.randn_like(logits)*F.softplus(noise_logits)
        # noisy_logits = logits + noise
        # top_k_logits, indices = noisy_logits.topk(self.top_k, dim=-1)

        # 获取前K大的值和索引，沿列。
        top_k_logits, indices = logits.topk(self.top_k, dim=-1)
        # 创建一个形状和logits相同全'-inf'矩阵，即(2,4,4)
        zeros = torch.full_like(logits, float('-inf'))
        # 按照索引和值填充上述zeros矩阵
        sparse_logits = zeros.scatter(-1, indices, top_k_logits)
        # 对其进行softmax，未被填充的位置会为0
        router_output = F.softmax(sparse_logits, dim=-1)
        return router_output, indices

代码中注释掉的部分是添加噪声的部分，有时候在训练过程中，某一个专家总是会被选择，而其余专家都很悠闲，我们不希望这种情况发生。上面代码注释掉的部分即是通过添加一些随机的噪声来影响输出的概率分布，希望在开始的时候为专家的选择添加一些随机性。

负载均衡

在通常的混合专家模型 (MoE) 训练中，门控网络往往倾向于主要激活相同的几个专家。这种情况可能会自我加强，因为受欢迎的专家训练得更快，因此它们更容易被选择。这种情况是我们不愿意看到的，因为这样其余的专家得不到充分的训练，没有达到我们想要的”不同的专家处理不同领域的问题”的初衷。同时从硬件角度来讲，不同的专家网络分布在不同的设备，训练不充分导致硬件资源利用率很低。

为了缓解这个问题，引入了一个辅助损失，旨在鼓励给予所有专家相同的重要性。这个损失确保所有专家接收到大致相等数量的训练样本，从而平衡了专家之间的选择。其中一种比较简单的辅助损失函数如下：

其中几个参数的含义如下：

$f_i$: 路由到第i个专家的比例
$s_{i, t}$: 表示第t个token选择第i个专家的概率
$P_i$: 表示第i个专家在这一整个序列中被选择的概率的平均值
$\alpha$是一个系数

由于$f_i$是不可微分的，所以最小化上面这个损失函数等价于最小化 $s_{i, t}$，对$s_{i, t}$的调整也会影响到$f_i$，最终调整分配给每个专家的负载。上述辅助损失和模型的交叉熵损失是添加在一起的。如下式：

$$
L_{total} = L_{main} + \lambda \cdot L_{balance} \tag{1.3}
$$

然而，使用这种辅助损耗来平衡负载是有代价的，因为其梯度可能会干扰语言建模目标的梯度，导致模型性能下降，综上所述，辅助损耗控制的负载均衡是一把双刃剑，如果alpha值未经仔细调整，可能会对模型性能产生负面影响。在实际应用中，由于资源限制，在大型语言模型训练期间调整alpha值具有挑战性，这进一步增加了优化过程的复杂性。

Deepseek中的专家架构

Deepseek-V3中使用的MoE架构可以说是业界比较前沿的架构了。它继承自deepseek-v2，主要有两个亮点，第一个即是使用了路由专家和共享专家的概念。如下图所示：

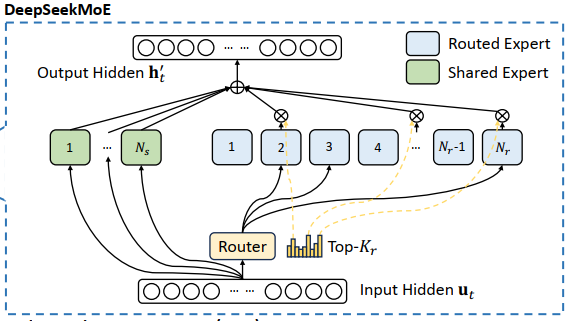
可以看到，所有token都会进入共享专家，所有token也都会进入路由(Router)，而Router最终会决定这些token各自进入哪一个专家。Deepseek的每一个MoE层会有256个路由专家，包含一个共享专家。其核心计算方法如论文中的公式如下：

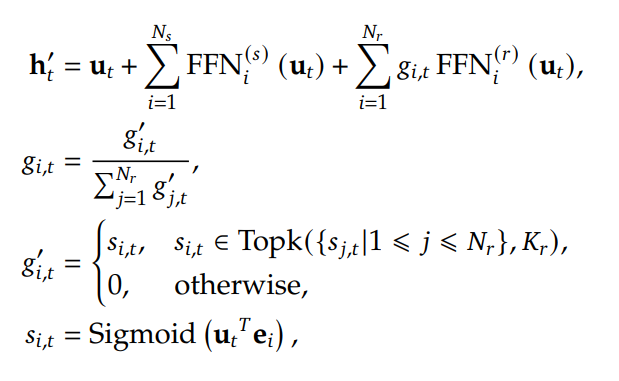
其中$u_t$表示当前序列中的第t个token的语义向量。由第一个公式可知，该token会经过所有的共享专家。$N_s$表示共享专家的个数。同时也会经过router为其选择topK个路由专家。$N_r$为路由专家的数量。最终token原本的向量和上面这两个结果加载一起构成MoE层对于单个token的输出。

最后一个公式$s_{i, t}$表示第t个token对应第i个专家的概率，第三个公式表明，处了被选中的topk个专家，其余专家的概率都为0。第二个公式表示被选中的专家的的结果加权求和时的权重。

无损失负载均衡策略

Deepseek采用了两种负载均衡方法，第一种是没有辅助损失函数的。即在门控网络的输出经过softmax之后的概率上加一个偏差，如下图所示：

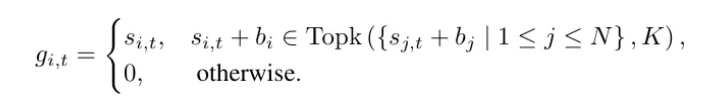
这个偏置的逻辑是，如果某些专家被过度选择，则偏置会变为负数从而降低专家被选择的概率。如果某些专家过于闲置，则偏置为负数，提高其被选择的概率。具体计算方式为：

首先计算每个专家分配的token数量的平均值
计算每个专家分配的标记数量，利用平均值减去该数量
偏差由该差值（或误差）的符号乘以一个固定的更新率决定，更新率是一个可调的超参数。
由此可见，如果一个专家被过度选择，则这个差值则为负数。如下所示：

当然了，Deepseek同样也使用了辅助损失函数，这个函数和上面提到的辅助损失函数形式比较像，我先研究研究再说。

MoE的优点

第一个显而易见的则是我们使用它的初衷，不同的FFN层处理不同的任务，我们希望对于一个token序列，每个专家擅长处理不同方面的语义，不同的专家可以学习到不同的特征，从而使得模型能更精细的处理更复杂的输入。
模型容量得到大大扩展。MoE 允许模型拥有大量的参数（每个专家都有自己的参数），而每个输入只需激活少量专家。通过增加专家数量，可以显著扩展模型的参数量，而不会显著增加计算成本（因为每个输入只激活少数几个专家）。

参考资料

DeepSeek-V3 的 MoE 架构解析：细粒度专家与高效模型扩展

[Deepseek v3技术报告学习] 2.MoE结构及MoE的负载均衡

DeepSeek-V3 解读3：无辅助损耗的负载均衡

混合专家模型 (MoE) 详解

从零实现一个MOE（专家混合模型）