punchy
Stay foolish Stay hungry

拼多多笔试

2025-07-04 算法

第一题

拉火车

每个人都有一副牌的一半，即26张，两个人玩拉火车的游戏，即轮流出牌，两个人分别叫alice和bob，轮流出牌构建一个序列，如果某个人出牌A时，前面的序列中有这张牌A1，则这个人将A1-A之间包括A1,A所有牌都收走，下一个人继续出牌。最后直到走完26张牌则游戏结束。结束时候比较谁的牌多即谁胜出。

我的解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import sys

T = int(sys.stdin.readline().strip())

for _ in range(T):
    a = list(map(int, sys.stdin.readline().strip().split()))
    b = list(map(int, sys.stdin.readline().strip().split()))
    train_list = []
    alice_hold_cards = 26
    bob_hold_cards = 26
    for i in range(len(a)):
        # alice 出牌
        cur_alice_card = a[i]
        if cur_alice_card not in train_list:
            train_list.append(cur_alice_card)
        else:
            index = train_list.index(cur_alice_card)
            alice_hold_cards = len(train_list[index:]) + 1
            train_list = train_list[:index]
        
        ## bob出牌
        cur_bob_card = b[i]
        if cur_bob_card not in train_list:
            train_list.append(cur_bob_card)
        else:
            index = train_list.index(cur_bob_card)
            bob_hold_cards = len(train_list[index:]) + 1
            train_list = train_list[:index]
        ## 如果此次出牌收牌了，则收的时候多加了一个1，这里减掉，数量时对的
        ## 如果此次出牌没有手牌，则手里的牌数要减1
        alice_hold_cards -= 1
        bob_hold_cards -= 1
    
    ## 每轮结束，判断谁的手牌数量多
    if alice_hold_cards > bob_hold_cards:
        print("Alice")
    elif alice_hold_cards < bob_hold_cards:
        print("Bob")
    else:
        print("Draw")

上述代码有一个可以优化的点时，index()操作是O(n)复杂度，因为列表的元素是按照顺序存储的，index方法会遍历列表，找到对应元素的索引。同样的方法还有x in list, list.remove(), list.count(x)均需要遍历列表。

如果我们将train_list即火车的序列使用字典来保存，键即牌的大小，值即牌的位置，这样既可以判断新的牌是否重复，也可以很快的用键来求得重复牌在火车中的位置，由键-》值这一过程是O(1)复杂度的

优化后代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import sys

T = int(sys.stdin.readline().strip())

for _ in range(T):
    a = list(map(int, sys.stdin.readline().strip().split()))
    b = list(map(int, sys.stdin.readline().strip().split()))

    card_pos = dict()
    train = []
    alice_cards = 26
    bob_cards = 26

    for i in range(26):

        card = alice_card(i)
        if card not in card_pos:
            train.append(card)
            card_pos[card] = len(train) - 1
            alice_cards -= 1
        else:
            cur_pos = card_pos[card]
            alice_cards += len(train[cur_pos:])
            for c in train[cur_pos:]
                card_pos.pop(c)
            train = train[:cur_pos]
        
        # Bob 出牌
        card = b[i]
        if card not in card_pos:
            train.append(card)
            card_pos[card] = len(train) - 1
            bob_cards -= 1
        else:
            cur_pos = card_pos[card]
            bob_cards += len(train[cur_pos:])
            for c in train[cur_pos:]:
                card_pos.pop(c)
            train = train[:cur_pos]

    if alice_cards > bob_cards:
        print("Alice")
    elif alice_cards < bob_cards:
        print("Bob")
    else:
        print("Draw")

去首都的最短距离(Dij)

AI解法

假如1号城市是首都，一共有n个城市，预先铺好了n-1条道路，还有两个城市之间没有道路，这两个城市之间将要铺一条道路，所有道路的长度都为1m，问，铺完这个将要铺道路的城市之后，所有城市和首都之间的最短距离是多少？

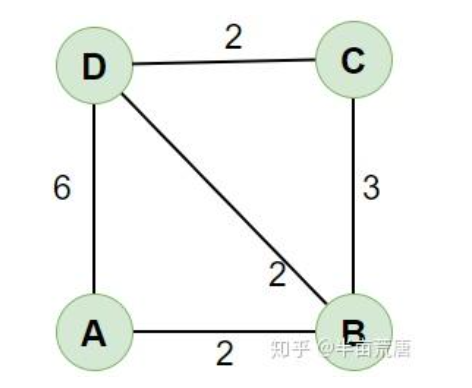
这道题明显要用到Dijkstra算法，首先要了解图这一个数据结构，即由顶点和边构成的一种图结构，边可以代表一定的长度，我们如何表示这个图结构呢？可以使用邻接矩阵的方式，即使用矩阵来表示一个图。假如一个图由四个顶点，如下图所示：

MLP层

使用邻接矩阵来表示即为：

1
2
3
4
5
int[][] graph = new int[][]{
{0 , 2, ∞, 6}
{2 , 0, 3, 2}
{∞ , 3, 0, 2}
{6 , 2, 2, 0}}

（0，0）表示A与A之间的距离，（0，1）表示A与B之间的距离，依次类推。图的边上的数字不仅可以表示为距离，还可以表示为耗时，网络延迟，所有我们统称为权重

如果我们以A为原点，想求出A点到其余所有点之间的距离，该怎么做呢？

这里需要介绍一个堆的概念，堆其实是二叉树的一种，不同的是堆的值是满足一定的规律的。以小顶堆为例，其定义是每一个节点的值都不大于其左右孩子节点的值。大顶堆则相反，每一个节点的值都不小于其左右孩子节点的值。那么这就造成了一个因素，如果我们定义元素出堆只能从堆顶元素出去的话，那么元素出去之后对于小顶堆来说，即构成一个递增序列， 从小到大排列。

  • 建堆：我们可以使用元素一个一个进行建堆如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
a = []
import heapq

heapq.heappush(a, 18)
heapq.heappush(a, 1)

a

[1, 18]

a = [3, 5, 6]

heap.heapify(a)
  • 出堆：从堆顶剔除元素
1
heapq.heappop(a)

dijkstra算法的核心是维护两个结果，一个result是已经求出最小路径的顶点，另一个是还没有求出最小路径的顶点notfound，里面的值都是到终点的距离。

最开始result中只有A点，因为A是起点，所有result = A(0),而notFound={B(2),C(∞),D(6)}.在未求出最小路径的点中，我们选一个距离最小的点B，到达B点后，那么A-B的最小路径已经求得，更新result为：result={A(0),B(2)}, notfound为：notFound={C(∞),D(6)}此时计算B点到其余点的距离，即更新notfound为：notFound={C(5),D(4)}，这时我们再找一个路径最短的点D，走到D点，更新result为：result={A(0),B(2),D(4)}，此时notfound为：notFound={C(5)},此时我们刷新距离D-》C的距离为2加上D-》A的距离6大于此时C存储的最短距离5，所以不更新。

核心思想是，每次到达一个新的点，我们都要计算其余点与此时点的距离，比较存储的的其余点距离起点的距离，保留更小的那个值。每次要出发下一个点时，要选择距离最短的那个，这样能保证到达该点后所走的路程就是起点距离该点最短的距离。

建图

第一步都是根据问题，建立图结构。比如以上面的图为例，我们可以构建图结构如下：

1
2
3
4
5
6
7
## 1,2,3,4 分别表示A,B,C,D      
graph = {
    1: [(2, 2), (4, 6)],       # A: B(2), D(6)
    2: [(1, 2), (3, 3), (4, 2)], # B: A(2), C(3), D(2)
    3: [(2, 3), (4, 2)],       # C: B(3), D(2)
    4: [(1, 6), (2, 2), (3, 2)]  # D: A(6), B(2), C(2)
}

初始化距离

使用一个字典表示每个点和起点的距离。初始默认为无穷大。

1
2
3
4
5
start = 1
## distances中存储所有点与起点的最短距离，所以初始化为无穷大
distances = [node: float('inf') for node in graph]

distances[start] = 0

构建一个优先级队列， 这个队列的优先级是根据相邻节点距离当前节点的距离来排序的，距离越小的越在前面，则越容易先被pop出来

1
priority_queue = [(0, start)]  ## 第一个元素表示当前节点和起点的距离，初始时，起点和起点之间的距离为0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
while priority_queue:
    cur_dist, cur_node = heapq.heappop(priority_queue)

    if cur_dist > distances[cur_node]:
        continue
    
    for nerbor, weight in graph[cur_node]:
        dictance = cur_dist + weight
        if dictance < distances[cur_node]:
            distances[nerbor] = distance
            ## 小顶堆构建的时候，如果插入的是元组，则首先比较第一个元素，若相同，再比较第二个元素
            ## 这里将当前节点的相邻节点插入到小顶堆中时，会根据每个相邻节点计算出来的新的距离来排序，最近的节点会别放在堆顶
            heapq.heappush(priority_queue, (distance, nerbor))
    
return distances

移动路径上的值按位与的最大结果

假设有一个矩阵，我们从左上角移动到右下角，每次只能移动一步，而且只能向右移动和向下移动，路径上的遇到的所有数，都执行与运算，问最大的值是多少？

📌 示例 1

矩阵：
[ [5, 4],
[7, 6] ]

所有可能路径及与运算过程：

  1. 路径：5 → 4 → 6   5 & 4 & 6 = 4
  2. 路径：5 → 7 → 6   5 & 7 & 6 = 4

最大值：4

📌 示例 2

矩阵：
[ [7, 3, 2],
[5, 1, 9],
[6, 8, 4] ]

示例路径一：
路径：7 → 3 → 2 → 9 → 4
运算：7 & 3 & 2 & 9 & 4 = 0

示例路径二：
路径：7 → 5 → 6 → 8 → 4
运算：7 & 5 & 6 & 8 & 4 = 0

最大值：0

我的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import sys
import random
T = int(sys.stdin.readline().strip())


tmp = sys.stdin.readline().strip().split()
n, m = int(tmp[0]), int(tmp[1])
matrix = []
move_list = [(1,0), (0,1)]
for _ in range(n):
    tmp_list = [int(num) for num in sys.stdin.readline().strip().split(" ")]
    matrix.append(tmp_list)
max_result = 0
## 共有多少种可能
## 从左上角到右下角的路径

for _ in range(n * n):
    start_pos = [0, 0]
    end_pos = [n-1, m-1]
    cur_pos = start_pos
    last_num = matrix[0][0]
    cur_result = 0
    while cur_pos != end_pos:
        cur_move = random.choice(move_list)
        if cur_pos[0] + cur_move[0] >= n:
            cur_move = (0, 1)
        elif cur_pos[1] + cur_move[1] >= m:
            cur_move = (1, 0)
        cur_pos[0] = cur_pos[0] + cur_move[0]
        cur_pos[1] = cur_pos[1] + cur_move[1]
        cur_num = matrix[cur_pos[0]][cur_pos[1]]
        cur_result = cur_result & cur_num
        last_num = cur_num
    
    if cur_result > max_result:
        max_result = cur_result

print(max_result)

第三题 📌 题目描述：矩阵路径最大按位与值（随机模拟法）

给定一个大小为 n × m 的整数矩阵，每次从矩阵的左上角 (0,0) 出发，只能 向右或向下移动一步，直到走到右下角 (n-1,m-1) 为止。

路径上经过的所有元素，使用按位与运算（bitwise AND）进行连续运算，最终得到一个路径结果值。请你通过模拟多条合法路径，找出其中按位与结果最大的那一条路径，并返回其值。

输入格式

  • 第一行一个整数 T，表示测试组数（当前代码中未使用）
  • 第二行两个整数 n 和 m，表示矩阵的行列数
  • 接下来的 n 行，每行包含 m 个整数，表示矩阵的内容

输出格式

  • 输出一个整数，表示模拟过程中所有路径的按位与结果中的最大值

我的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import sys
import random
T = int(sys.stdin.readline().strip())


tmp = sys.stdin.readline().strip().split()
n, m = int(tmp[0]), int(tmp[1])
matrix = []
move_list = [(1,0), (0,1)]
for _ in range(n):
    tmp_list = [int(num) for num in sys.stdin.readline().strip().split(" ")]
    matrix.append(tmp_list)
max_result = 0
## 共有多少种可能
## 从左上角到右下角的路径

for _ in range(n * n):
    start_pos = [0, 0]
    end_pos = [n-1, m-1]
    cur_pos = start_pos
    last_num = matrix[0][0]
    cur_result = 0
    while cur_pos != end_pos:
        cur_move = random.choice(move_list)
        if cur_pos[0] + cur_move[0] >= n:
            cur_move = (0, 1)
        elif cur_pos[1] + cur_move[1] >= m:
            cur_move = (1, 0)
        cur_pos[0] = cur_pos[0] + cur_move[0]
        cur_pos[1] = cur_pos[1] + cur_move[1]
        cur_num = matrix[cur_pos[0]][cur_pos[1]]
        cur_result = cur_result & cur_num
        last_num = cur_num
    
    if cur_result > max_result:
        max_result = cur_result

print(max_result)

我的代码纯靠概率，每次向下或向右随机选一步，直到到达终点，这就算一次尝试，记录这次尝试的结果。那么多少次尝试就能找到最大值呢，这里我一般设计为矩阵的行数或者列数的次方的最大值。所以是比较靠运气的。提交的时候有一般的测试用例没有通过。

动态规划的方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import sys
import random
T = int(sys.stdin.readline().strip())

tmp = sys.stdin.readline().strip().split()
n, m = int(tmp[0]), int(tmp[1])
matrix = []

for _ in range(n):
    tmp_list = [int(num) for num in sys.stdin.readline().strip().split(" ")]
    matrix.append(tmp_list)

dp = [[0] * m for _ in range(n)]
dp[0][0] = matrix[0][0]

for i in range(n):
    for j in range(m):
        if i == 0 and j == 0:
            continue
        if i == 0:
            ## 第0行的每个元素只能是通过向右走走到这里的，所以和左边的上一个元素进行与运算
            dp[i][j] = dp[i][j] & dp[i][j - 1]
        if j == 0:
            ## 第0列的每个元素只能是通过向下走走到这里的，所有和上边的上一个元素进行与运算
            dp[i][j] = dp[i][j] & dp[i - 1][j]
        else:
            ## 不是第0行和第0列的元素，就找他的上边的元素和左边的元素的与运算的最大值
            dp[i][j] = max(dp[i][j] & dp[i - 1][j], dp[i][j] & dp[i][j -1])
            ## 所以dp数组每个位置的值保存的是当到达当前位置时，进行与运算的结果的最大值，那么我们一直求，直到求出右下角元素的值，就可以直到从左上角到右下角的与运算最大值，同时也知道了从左上角到任何一个点的与运算的结果的最大值

print(dp[n - 1][m - 1])

📝 题目描述

多多最近喜欢玩一款游戏，游戏中共有 n 个关卡，每个关卡各自的难度等级，并且这款游戏很有趣，游戏过程中开出来的关卡难度不是由简单到难，有可能第 i 关难度为 5，而第 i+1 关难度为 2。多多在通关之后想复盘某些关卡精进游戏技巧，好在这款游戏提供了方便的复盘路径，可以指定区间以及最低的难度值 min_d，这段区间中所有难度值大于等于 min_d 的关卡都将被选中。

已知多多选出来的 m 段关卡序列情况，请你推测这款游戏的 n 个关卡至少要划分为多少个不同的难度等级才能满足 m 段关卡都符合上述要求。

🔢 输入描述

  • 第一行一个整数 T，表示共计 T 个测试数据（1 ≤ T ≤ 10）
  • 每组测试数据：
    • 第一行两个整数 n 和 m，分别表示游戏关卡总数和多多选择的复盘序列段数（1 ≤ n, m ≤ 1000）
    • 第二行 n 个整数 a_1, a_2, ..., a_n，表示编号为 1 ~ n 的每个关卡是否被选中，1 表示选中，0 表示没有被选中
    • 接下来 m 行，每行两个整数 [a, b]，表示某段关卡区间 [a, b]（题目保证 1 ≤ a < b ≤ n）

📤 输出描述

每组数据输出一个结果，每个结果占一行，表示最少需要多少种不同的难度等级的划分，才能满足每段 [a, b] 区间中选中的关卡是这段区间中所有大于等于某个 min_d 的所有关卡。

💡 补充说明

  • 对于 20% 的数据：1 ≤ n, m ≤ 10
  • 对于 60% 的数据：1 ≤ n, m ≤ 100
  • 对于 100% 的数据：1 ≤ n, m ≤ 1000

输入：

1
2
3
4
5
1
3 2
1 0 1
1 2
2 3

输出：
2

📎 提示

题目保证每段 [a, b] 中选中的关卡，一定满足存在一个 min_d，使得区间中所有大于等于 min_d 的关卡，正好对应这些被选中的位置。

这题有点难，设计拓扑排序，暂时搁置一下。

Author: 武丢丢

Link: http://example.com/2025/07/04/%E6%8B%BC%E5%A4%9A%E5%A4%9A%E7%AC%94%E8%AF%95/

Copyright: All articles in this blog are licensed under CC BY-NC-SA 3.0 unless stating additionally.

NextPost >
uv_learn
CATALOG
  1. 1. 第一题
    1. 1.1. 拉火车
      1. 1.1.1. 我的解法
    2. 1.2. 去首都的最短距离(Dij)
      1. 1.2.1. AI解法
      2. 1.2.2. 建图
      3. 1.2.3. 初始化距离
    3. 1.3. 移动路径上的值按位与的最大结果
    4. 1.4. 📌 示例 1
    5. 1.5. 📌 示例 2
      1. 1.5.1. 我的代码
    6. 1.6. 第三题 📌 题目描述：矩阵路径最大按位与值（随机模拟法）
      1. 1.6.1. 输入格式
      2. 1.6.2. 输出格式
        1. 1.6.2.1. 我的代码
        2. 1.6.2.2. 动态规划的方法
    7. 1.7. 📝 题目描述
    8. 1.8. 🔢 输入描述
    9. 1.9. 📤 输出描述
    10. 1.10. 💡 补充说明
      1. 1.10.1. 📎 提示